作者: 必考單元-拋物線
國中會考的拋物線，是每年的必考題
但即便是拋物線這個小單元，它的答對率還是偏低。
110答對率為44%
109答對率為33%
108答對率為40%。
那既然單元的範圍不大，如果可以搞懂它的考點
是不是就代表會考的分數穩穩的多對了一題?
拋物線核心重點
二元一次方程式?聽起來有夠抽象
但在國中，討論的大多只是拋物線而已
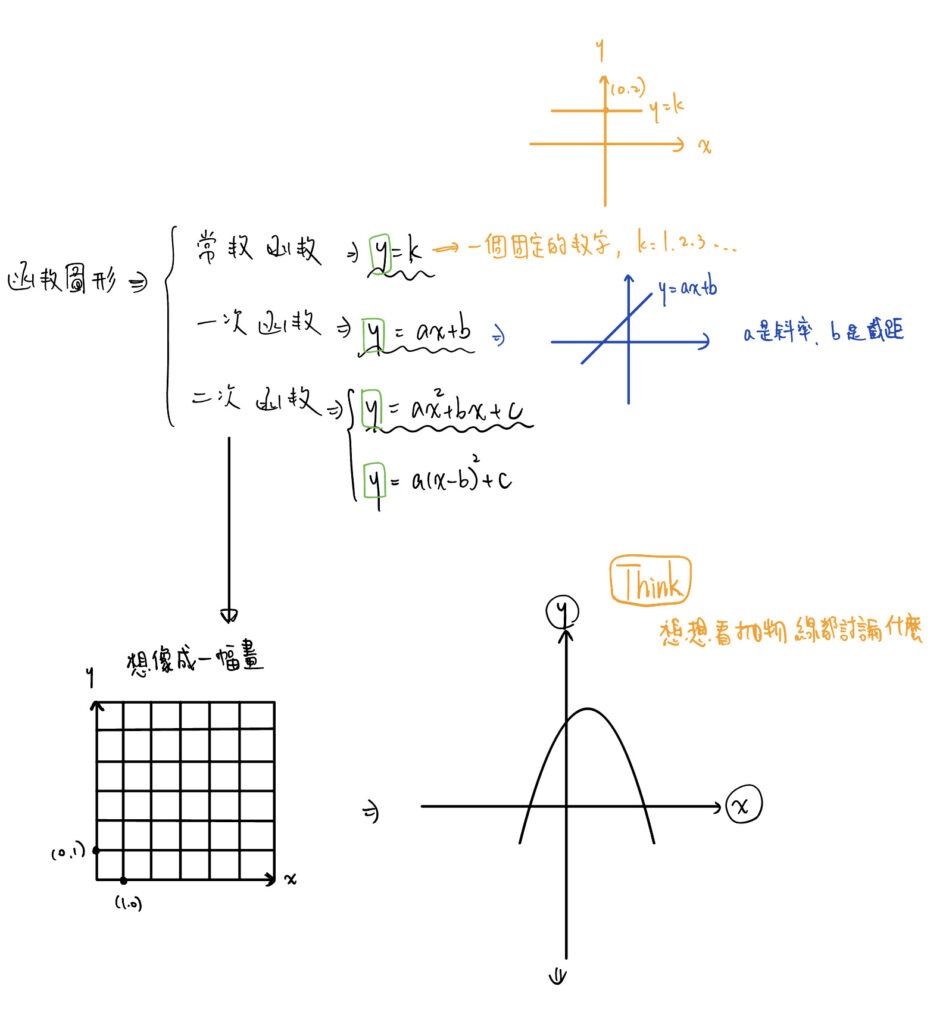
上面快速討論了常數函數、一次函數、二次函數
但我今天先討論二次函數，究竟這個拋物線的重點是什麼呢?
拋物線會考的重點只有一個，就是搞清楚拋物線的標準式y=a(x-b)2+c
一般來說，題目給我的條件通常會是y=ax2+bx+c，在這個步驟我們能得到的資訊比較少
因此我們會先轉換成由標準式y=a(x-b)2+c
我們可以知道他的對稱軸、頂點、開口方向及大小，
最後搭配和x軸、y軸的交點，那百分之95的題目都會搞定。
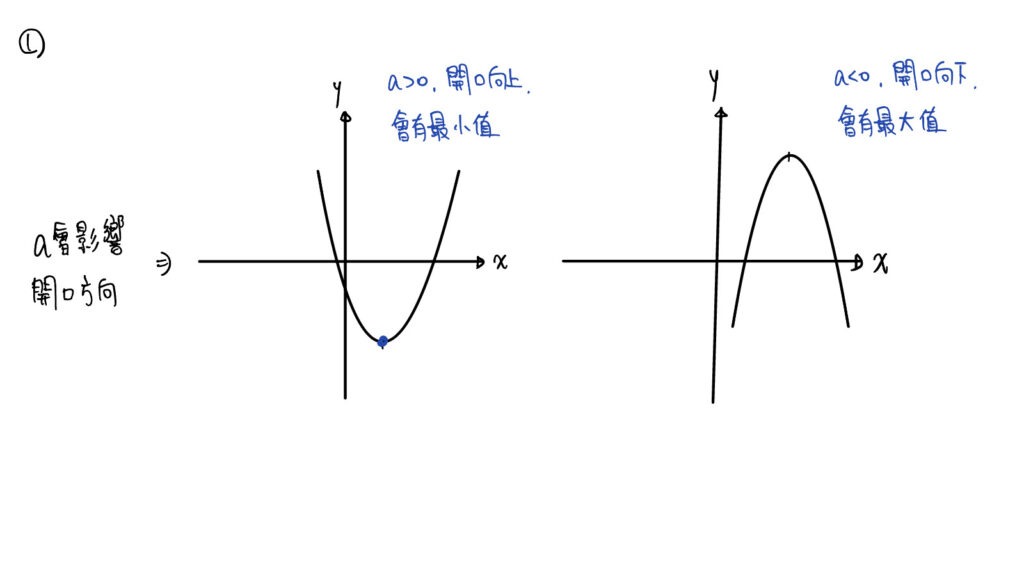
拋物線的開口方向
開口方向，會由a來決定會代表開口方向及開口大小
注意，這個a是y=a(x-b)2+c，當然也是y=ax2+bx+c
圖形如下
拋物線和x軸的交點
這個就會講到進階一點的判別式，高中很多的考題都會用到
有些國中比較難的題目也會說到一些
這邊當大家做個補充
判別式是b2-4ac，這邊的a,b,c指的是y=ax2+bx+c的a,b,c
藉由b2-4ac是否大於0、等於0、小於0，來去快速判斷它和x軸的交點數
很多人認為它是一個公式
但我真心地給大家一個建議，如果你的目標是高分群
那就自己親自去證明它
因為當你在正名的過程中，你可以搞清楚很多原來不會的盲點
像是拋物線轉換成標準式的計算，又或者是增加你解方程式的能力
這樣不管題目怎麼換，你都擁有比別人更強的實力
這也是我一直強調的，新課綱，就是新瓶裝舊酒
把舊有的觀念地滾光爛熟
才是對付新課綱的最好方式
所以，如果你看到拋物線的題目，還是覺得有點抖抖的，不妨先先把題目給的二次函數化為標準式，仔細從對稱軸、頂點、開口方向，x軸、y軸的交點來思考。
我知道上面講的很抽象，所以如果你想看影片的呈現方式，請點及下方連結
最後，如果想知道更多的考試技巧
歡迎追蹤fb或ig
